
Сложный ряд Фурье – это одна из основных тем, которую изучают при изучении математики и физики. Он является мощным инструментом для разложения сложных функций на более простые составляющие. Но работать с ним может быть сложно, особенно для начинающих студентов.
В этом руководстве мы рассмотрим основные ошибки, которые могут возникнуть при расширении сложного ряда Фурье в Python. Мы подробно рассмотрим каждую ошибку и предоставим примеры кода, чтобы помочь начинающим программистам разобраться в этих проблемах.
Знание этих ошибок и умение предотвращать их – важные навыки, которые помогут вам развиться в программировании. Если вы хотите освоить расширение сложного ряда Фурье в Python, это руководство станет для вас отличным первым шагом на пути к освоению этой мощной техники.
- Что такое расширение сложного ряда Фурье?
- Определение расширения сложного ряда Фурье
- Применение расширения сложного ряда Фурье в Python
- Ошибки при применении расширения сложного ряда Фурье
- Руководство по предотвращению ошибок
- Установка и подключение библиотеки для работы с расширением сложного ряда Фурье
- Изучение документации и примеров кода
Что такое расширение сложного ряда Фурье?
Сложный ряд Фурье может быть представлен в виде:
| f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty} (a_n \cos(nx) + b_n \sin(nx)) |
где f(x) — периодическая функция с периодом 2π, a_0, a_n и b_n — коэффициенты Фурье, которые можно вычислить с помощью интегралов.
Расширение сложного ряда Фурье позволяет приближенно представить сложную периодическую функцию в виде суммы гармоник, что облегчает ее анализ и обработку. Этот метод широко применяется в различных областях науки и техники, таких как теория управления, обработка сигналов, оптика, теория информации и др.
Определение расширения сложного ряда Фурье

Применяется в математическом анализе и теории сигналов, метод ряда Фурье позволяет представить периодическую функцию в виде суммы синусов и косинусов. Расширение сложного ряда Фурье позволяет аппроксимировать не только периодические функции, но также и не периодические функции путем добавления гармонических функций с различными частотами и амплитудами.
Расширение сложного ряда Фурье является важным инструментом в обработке сигналов, анализе спектров и дискретной математике. Оно используется в таких областях, как компьютерная графика, обработка изображений, аудио-сжатие и связанные с ними технологии.
Преимущества:
- Аппроксимация непериодических функций
- Гибкость настройки
- Широкое применение в различных областях
Использование расширения сложного ряда Фурье помогает получить адекватные приближения сложных функций и упростить их дальнейший анализ.
Применение расширения сложного ряда Фурье в Python
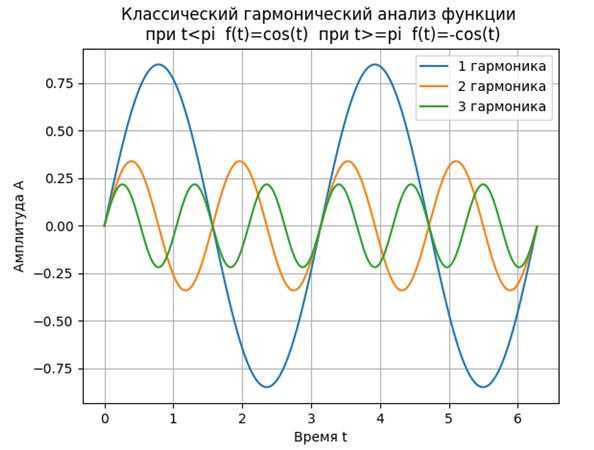
Одним из самых популярных инструментов для работы с рядами Фурье в Python является библиотека NumPy. Она предоставляет функции для вычисления коэффициентов ряда Фурье, а также для обратного преобразования. С помощью NumPy вы можете легко анализировать и модифицировать сигналы, а также визуализировать результаты.
Более того, расширение сложного ряда Фурье может применяться и в задачах машинного обучения. Например, преобразование Фурье может использоваться для извлечения признаков из изображений или звуковых файлов. Эти признаки могут быть затем использованы в алгоритмах классификации или регрессии.
Еще одним интересным применением расширения сложного ряда Фурье является компрессия данных. Поскольку ряд Фурье позволяет представить сложную функцию с помощью меньшего числа компонент, это может быть использовано для сжатия данных без значительной потери информации. Таким образом, расширение сложного ряда Фурье может быть полезным инструментом при работе с большими объемами данных, например, в области обработки видео.
| Преимущества применения расширения сложного ряда Фурье в Python |
|---|
| 1. Возможность анализа и обработки сложных сигналов и сигналов во временной и частотной области. |
| 2. Легкость использования библиотеки NumPy для работы с рядами Фурье. |
| 3. Возможность использования расширения сложного ряда Фурье в задачах машинного обучения. |
| 4. Возможность использования расширения сложного ряда Фурье для компрессии данных. |
Ошибки при применении расширения сложного ряда Фурье
Одна из распространенных ошибок, связанных с применением расширения сложного ряда Фурье, это неправильное определение коэффициентов Фурье для заданной функции или набора данных. Коэффициенты Фурье отражают вклад каждой гармоники в рассматриваемую функцию и необходимы для правильного восстановления функции из ее спектра. Если коэффициенты Фурье определены неверно, результаты могут быть искажены или неполными.
Другой распространенной ошибкой при использовании расширения сложного ряда Фурье является использование недостаточного количества гармоник при аппроксимации функции. Сложный ряд Фурье требует учета бесконечного числа гармоник для точного восстановления функции. Однако, в реальной практике обычно используется конечное число гармоник для приближенного представления функции. Если использовать недостаточное количество гармоник, результаты могут быть неточными или грубыми.
Также стоит быть внимательным при манипуляциях с Фурье-спектром или спектральным представлением функции. Фурье-спектр и спектральное представление функции могут быть сложными объектами, требующими особой обработки и понимания. Неправильные операции с Фурье-спектром могут привести к искажениям или потере информации о функции.
Для избежания этих и других ошибок при применении расширения сложного ряда Фурье в Python, важно иметь хорошее понимание теории расширения и необходимо тщательно проверять и тестировать свой код. Кроме того, наблюдение за результатами и анализ результатов могут помочь выявить и исправить ошибки на ранних этапах.
Руководство по предотвращению ошибок
1. Планирование перед написанием кода. Прежде чем начать писать код, важно провести тщательное планирование. Четко определите свои цели и требования к коду. Это поможет избежать некоторых ошибок, связанных с неправильным проектированием и архитектурой кода.
2. Использование современных инструментов разработки. Хороший редактор кода или интегрированная среда разработки (IDE) может значительно упростить процесс написания и отладки кода. Используйте инструменты, которые предлагают интеллектуальное автодополнение, подсветку синтаксиса и отладку кода.
3. Постоянная проверка качества кода. Проверяйте свой код на наличие потенциальных ошибок и неправильных практик. В Python существует множество инструментов статического анализа кода, которые могут автоматически обнаруживать проблемы. Постоянная проверка кода поможет предотвратить серьезные ошибки.
4. Тестирование кода. Тестирование является важной частью разработки программного обеспечения. Напишите автоматические тесты, которые проверяют, работает ли ваш код правильно в разных сценариях. Это позволит быстро обнаружить ошибки и разрешить их до запуска кода в реальной среде.
5. Контроль версий кода. Используйте систему контроля версий, такую как Git, для отслеживания изменений в вашем коде. Контроль версий позволяет вам хранить и отслеживать разные версии кода, а также быстро откатываться к предыдущим версиям в случае ошибок.
6. Запись ошибок. Если вы столкнулись с ошибкой или багом, запишите ее, а также шаги, которые привели к ее возникновению. Это поможет вам легко возвращаться к проблеме в будущем и избежать повторения ошибки.
7. Непрерывное обучение. Всегда стремитесь к улучшению ваших навыков программирования. Изучайте новые технологии и лучшие практики. Чем больше вы узнаете, тем меньше вероятность совершить ошибку.
Следуя этим руководствам, вы сможете предотвратить множество ошибок и улучшить качество вашего кода. Помните, что ошибки — нормальная часть процесса программирования, и важно уметь учиться на них и исправлять.
Установка и подключение библиотеки для работы с расширением сложного ряда Фурье
Для работы с расширением сложного ряда Фурье в Python, необходимо установить и подключить соответствующую библиотеку. В данном случае, мы будем использовать библиотеку numpy.
Для установки библиотеки numpy, можно воспользоваться менеджером пакетов pip, который входит в комплект поставки Python. Для этого необходимо выполнить следующую команду:
pip install numpy
После успешной установки библиотеки numpy, можно перейти к подключению ее в своем коде. Для этого необходимо добавить следующую строку в начало вашего скрипта:
import numpy as np
После добавления данной строки, вы сможете использовать функции и возможности, предоставляемые библиотекой numpy, в вашем коде.
Подключение и использование библиотеки numpy в ваших проектах позволит вам удобно и эффективно работать с расширением сложного ряда Фурье в Python.
Изучение документации и примеров кода
Для того чтобы изучить ошибки расширения сложного ряда Фурье в Python, важно обратить внимание на документацию и примеры кода. Python имеет обширную и хорошо документированную библиотеку, которая предлагает различные методы для работы с рядами Фурье.
Прежде чем приступить к изучению документации, рекомендуется иметь базовое понимание основных понятий и терминов, связанных с рядами Фурье. Также стоит обратить внимание на то, какие структуры данных и функции используются в Python для работы с рядами Фурье.
Документация является основным источником информации о доступных методах, аргументах и возможностях библиотеки. В документации можно найти детальное описание каждого метода, его синтаксис, аргументы и возвращаемые значения.
Помимо документации, полезно изучить примеры кода, которые демонстрируют применение различных методов и функций. Примеры кода могут помочь понять, как использовать методы правильно, а также показать возможные подводные камни.
Изучение документации и примеров кода является важным шагом в освоении расширения сложного ряда Фурье в Python. Это позволит лучше понимать возможности библиотеки и использовать ее эффективно для решения различных задач.



