Решение системы уравнений — одна из наиболее важных задач в математике и науке. Однако, когда имеем дело со сложными системами, содержащими нелинейные уравнения, задача становится намного сложнее. В этой статье мы рассмотрим методы решения систем из шести нелинейных уравнений с использованием Python и обсудим проблемы, с которыми можно столкнуться в процессе.
Python — мощный язык программирования, который позволяет легко и эффективно решать математические задачи. Для решения системы уравнений на Python мы можем использовать множество методов, таких как метод Ньютона, метод итерации, аналитическое решение и другие.
Одной из главных проблем при решении системы из 6 нелинейных уравнений является сложность самой системы. Чем больше уравнений и нелинейность, тем сложнее найти аналитическое решение. Однако, на помощь приходит Python, который позволяет нам использовать численные методы для приближенного решения системы.
Использование Python для решения системы из 6 нелинейных уравнений позволяет нам не только найти численное решение, но и провести анализ системы, убедиться в корректности найденного решения и, при необходимости, внести корректировки в уравнения или методы решения.
Возникшие проблемы при решении системы
При решении системы из 6 нелинейных уравнений на Python возможно возникновение нескольких проблем, с которыми стоит быть готовым к столкновению. Ниже представлены некоторые из них:
1. Сложность системы: Нелинейные системы уравнений могут быть очень сложными и содержать большое количество уравнений и неизвестных. Это может привести к высокому вычислительному времени и объему памяти, необходимому для их решения. Важно учитывать ограничения компьютерных ресурсов при работе с такими системами.
2. Необходимость выбора метода решения: Существует множество методов решения нелинейных систем уравнений, и правильный выбор метода может быть нетривиальной задачей. Разные методы имеют свои преимущества и недостатки, и не каждый метод подходит для решения конкретной системы. Изучение и анализ различных методов имеет большое значение для успешного решения задачи.
3. Невозможность нахождения аналитического решения: Некоторые системы уравнений могут быть настолько сложными, что аналитическое решение невозможно найти. В таких случаях требуется использование численных методов, которые могут быть более затратными с точки зрения времени и вычислительных ресурсов.
4. Сходимость метода: Конкретный метод решения может не обеспечивать сходимость к решению системы в определенных случаях. Сходимость — это способность метода приближаться к решению с заданной точностью. Если метод не сходится, то решение системы невозможно получить. Важно уметь определить, сходится ли выбранный метод для конкретной системы уравнений.
5. Неустойчивость решения: Некоторые методы могут быть неустойчивыми и приводить к большим ошибкам и погрешностям в результате. Это может быть вызвано численными проблемами или особенностями конкретной системы уравнений. При решении системы следует обращать внимание на устойчивость выбранного метода и возможность погрешностей в полученных результатах.
При решении системы из 6 нелинейных уравнений, важно учитывать вышеуказанные проблемы и выбирать наиболее подходящий метод решения в зависимости от конкретных условий задачи.
Выбор метода решения
Для решения системы из 6 нелинейных уравнений на Python необходимо выбрать подходящий метод. В данном случае можно использовать метод итераций или метод Ньютона.
Метод итераций подразумевает построение последовательности приближенных решений, которая сходится к точному решению системы. Для этого необходимо преобразовать систему нелинейных уравнений в эквивалентную систему линейных уравнений, и затем использовать итерационный процесс для приближенного нахождения решения.
Метод Ньютона предполагает аппроксимацию функций системы линейными функциями и последующее решение полученной линейной системы уравнений. Этот метод обеспечивает быструю сходимость к точному решению, но требует начальной точки и вычисление матрицы Якоби.
При выборе метода решения следует учитывать особенности системы уравнений и требуемую точность решения. Экспериментирование с разными методами и оценка их результатов могут помочь в выборе подходящего метода решения системы из 6 нелинейных уравнений на Python.
Точность вычислений
Точность вычислений играет важную роль при решении системы из 6 нелинейных уравнений на Python. Несмотря на то, что Python имеет высокую точность вычислений, возможны ошибки округления, которые могут привести к неточным результатам. Поэтому необходимо учитывать особенности работы с плавающей точкой и выполнять дополнительные проверки на точность вычислений.
Одним из способов повышения точности вычислений является использование библиотеки mpmath. Mpmath позволяет работать с произвольной точностью чисел с плавающей точкой и выполнять математические операции с высокой точностью. Эта библиотека может быть полезна при решении системы нелинейных уравнений, особенно если требуется высокая точность.
Для использования библиотеки mpmath необходимо установить ее с помощью менеджера пакетов pip. После установки можно импортировать библиотеку в свой проект и использовать ее функциональность для повышения точности вычислений.
Еще одним методом повышения точности вычислений является использование итерационных методов. Такие методы позволяют найти приближенное решение системы уравнений с заданной точностью. Например, метод Ньютона-Рафсона или метод простой итерации могут быть использованы для решения системы нелинейных уравнений на Python.
Однако необходимо помнить, что повышение точности вычислений может привести к увеличению времени выполнения программы. Поэтому рекомендуется балансировать между точностью вычислений и производительностью программы, особенно при работе с большими системами уравнений.
Общий подход к повышению точности вычислений при решении системы из 6 нелинейных уравнений на Python включает в себя: использование библиотеки mpmath для работы с высокой точностью чисел с плавающей точкой, применение итерационных методов для приближенного решения системы и балансирование между точностью и производительностью программы.
Необходимость предварительной обработки данных
Перед решением системы из 6 нелинейных уравнений, необходимо провести предварительную обработку данных. Этот этап позволяет улучшить качество и точность решения, а также упростить последующие шаги алгоритма.
Другой задачей предварительной обработки данных является выбор подходящего метода решения для данной системы уравнений. Некоторые методы могут быть более эффективными или точными при определенных условиях. Необходимо исследовать и анализировать данные, чтобы выбрать наиболее подходящий метод решения.
Кроме того, предварительная обработка данных включает в себя проверку на наличие нелинейных уравнений, которые могут оказаться неразрешимыми или требующими особого подхода. Некоторые уравнения можно преобразовать, линеаризовать или переформулировать, чтобы получить более простую систему уравнений.
Таким образом, необходимость предварительной обработки данных перед решением системы из 6 нелинейных уравнений заключается в улучшении качества решения, выборе подходящего метода решения и обнаружении и решении потенциальных проблем, связанных с нелинейностью уравнений.
Возможные решения проблем
Решение системы нелинейных уравнений может быть достаточно сложной задачей, но существуют несколько подходов, которые могут помочь упростить и ускорить процесс.
1. Метод пристального взгляда: Если система нелинейных уравнений содержит простые компоненты, то можно взглянуть на уравнения и попытаться заметить какие-либо закономерности или симметрии. Иногда такой «интуитивный» подход может привести к простому и эффективному решению.
2. Использование численных методов: Если система нелинейных уравнений сложная, то можно воспользоваться численными методами, такими как метод Ньютона или метод секущих. Эти методы позволяют приближенно найти решение системы, начиная с некоторой исходной точки.
3. Применение компьютерных программ: Для решения системы нелинейных уравнений на Python можно использовать различные библиотеки и пакеты, такие как SciPy или SymPy. Эти инструменты предоставляют готовые функции и методы для численного решения системы уравнений.
4. Проверка аналитического решения: Если система нелинейных уравнений имеет аналитическое решение, то его можно найти путем символьных вычислений используя символьные вычислительные пакеты, такие как SymPy. Полученное аналитическое решение можно затем проверить численно с помощью компьютерной программы.
5. Проверка геометрического решения: Иногда система нелинейных уравнений имеет геометрическое решение, то есть решение, которое можно представить в виде графика или геометрической конструкции. В таких случаях можно визуализировать уравнения и графически найти их точки пересечения.
Несмотря на то, что решение системы нелинейных уравнений может быть сложной задачей, существует множество подходов и инструментов, которые могут помочь в ее решении. Выбор конкретного метода зависит от сложности системы и доступных ресурсов, но с правильным подходом и использованием соответствующих инструментов, можно добиться успешного результата.
Использование численных методов
Решение системы из 6 нелинейных уравнений может быть сложной задачей, особенно при отсутствии аналитического решения. В таких случаях можно использовать численные методы, которые позволяют приближенно найти значения переменных, удовлетворяющие системе уравнений.
Один из основных численных методов, который может быть применен к системе нелинейных уравнений, это метод Ньютона. Он основан на принципе локальной линеаризации функций и итерационного приближения. Данный метод требует наличия начального приближения и предполагает использование производных функций. Для его реализации можно воспользоваться уже готовыми библиотеками, такими как SciPy.
Еще одним популярным численным методом является метод секущих. В отличие от метода Ньютона, он не требует знания производных функций и прост в реализации. Вместо этого метод использует разности значений функций в двух точках и их отношения для приближенного нахождения решения системы. Этот метод также можно использовать с помощью библиотеки SciPy.
Существует множество других численных методов, которые могут быть применены к решению системы нелинейных уравнений. Некоторые из них включают метод половинного деления, метод секущих второго порядка и метод Рунге-Кутты. Выбор метода зависит от конкретной задачи и требований к точности и скорости вычислений.
При использовании численных методов нелинейные системы уравнений можно решать в программных средах, таких как Python, с помощью соответствующих библиотек. Наличие готовых реализаций методов упрощает процесс решения и позволяет получить результаты быстрее.
Таким образом, использование численных методов является эффективным подходом к решению системы из 6 нелинейных уравнений, особенно в случаях, когда аналитическое решение неизвестно или его получение затруднительно.
Увеличение точности вычислений
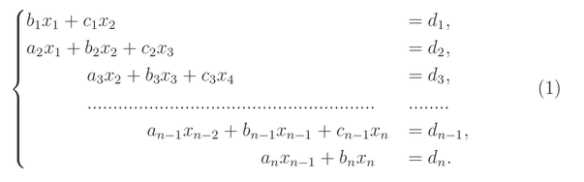
Для увеличения точности вычислений можно использовать различные методы:
- Использование библиотеки decimal: библиотека decimal в Python позволяет работать с числами с фиксированной точностью, что дает более точные результаты при выполнении математических операций.
- Применение метода Ньютона: метод Ньютона является итерационным методом решения систем уравнений и позволяет достичь более точных результатов. Он основан на линеаризации нелинейной системы и последовательном пересчете значений переменных.
- Уточнение начальных приближений: точность результата может быть увеличена путем более точного определения начальных приближений для переменных. Для этого можно использовать предварительные вычисления или аналитический подход.
- Использование высокоточного представления чисел: в Python существуют специальные структуры данных, такие как модуль fractions или тип Decimal, которые позволяют работать с числами с высокой точностью.
Применение этих методов позволяет увеличить точность вычислений и получить более точный результат при решении системы из 6 нелинейных уравнений на Python.
Предварительная обработка данных
Перед решением системы из 6 нелинейных уравнений на Python необходимо провести предварительную обработку данных. Этот этап поможет убедиться в правильности введенных данных и подготовить их к дальнейшему анализу.
Важным шагом предварительной обработки данных является проверка их корректности. Необходимо убедиться, что все уравнения были правильно записаны и введены без ошибок. Для этого можно использовать регулярные выражения или другие методы проверки текста.
Далее следует провести анализ данных и их очистку от выбросов или некорректных значений. Методы статистики и визуализации данных могут помочь выявить аномальные значения или шумы. Также можно использовать фильтры или другие алгоритмы для удаления выбросов.
После того как данные были проверены и очищены, следует провести их нормализацию или стандартизацию. Это поможет привести значения к одному масштабу и облегчить дальнейший анализ. Нормализацию можно выполнить с помощью методов минимакса или Z-оценки.
Важным этапом предварительной обработки данных является также выбор подходящих методов решения системы из 6 нелинейных уравнений. В зависимости от характера данных и требуемой точности, можно выбрать различные алгоритмы численного решения, такие как метод Ньютона или метод секущих.
В итоге, предварительная обработка данных позволяет избавиться от ошибок, очистить данные от выбросов и некорректных значений, нормализовать их, а также выбрать подходящие методы решения системы уравнений. Это значительно повышает точность и надежность полученных результатов.



