Python является мощным инструментом, который может быть использован для обработки и анализа аудио данных. Одним из важных инструментов в анализе аудиофайлов является преобразование Фурье (FFT) — способ перевода сигнала из временного представления в частотное представление.
Преобразование Фурье позволяет разложить сигнал на набор гармонических компонент, что позволяет легко анализировать спектральные характеристики звука. В Python существует ряд библиотек и функций, которые облегчают работу с FFT и делают его доступным для широкой аудитории.
Одной из самых популярных библиотек для работы с FFT в Python является библиотека NumPy. NumPy предоставляет множество функций для работы с массивами и матрицами, включая функции FFT. Эти функции позволяют легко применять преобразование Фурье к аудиофайлам и анализировать их спектральные характеристики.
FFT также широко применяется в области обработки звука и сигналов. Например, с его помощью можно сделать аудио анализатор или эквалайзер, который позволяет позволяет отобразить частотные компоненты аудиосигнала и регулировать уровень громкости для каждой частотной полосы отдельно. Также это может быть полезным при обработке звука в реальном времени, например, при фильтрации нежелательных шумов или эффектов.
- Раздел 1: Понятие FFT в аудиообработке
- Определение и суть FFT
- Различия между FFT и DFT
- Преобразование временной области в частотную область с помощью FFT
- Раздел 2: Основные методы FFT в Python
- Библиотеки и модули Python для работы с FFT
- Примеры кода на Python для реализации FFT
- Настройка параметров FFT для оптимального анализа аудиофайлов
- Раздел 3: Применение FFT в аудиообработке
Раздел 1: Понятие FFT в аудиообработке
FFT работает на основе теории Фурье, которая утверждает, что любой периодический сигнал можно представить как сумму гармонических функций различных частот и амплитуд. В аудиообработке, сигналы записываются в цифровой форме, и FFT позволяет анализировать эти цифровые сигналы для вычисления их спектральных характеристик.
FFT преобразование применяется в различных областях аудиообработки:
| 1. Спектральный анализ | – FFT позволяет анализировать спектры звуковых сигналов, вычислять частоты, амплитуды и фазы компонентов сигнала. |
| 2. Фильтрация | – FFT позволяет применять различные фильтры к аудиосигналам, такие как фильтры низких или высоких частот. |
| 3. Компрессия | – FFT применяется в аудио компрессии для уменьшения размера файла, удаляя ненужную информацию из спектра сигнала. |
| 4. Синтез звука | – FFT позволяет создавать новые звуки, комбинируя различные компоненты спектра сигналов. |
| 5. Эффекты | – FFT преобразование используется в процессе создания звуковых эффектов, таких как эхо, реверберация, и др. |
Определение и суть FFT

Преобразование Фурье позволяет разложить функцию на сумму гармонических компонент с различными амплитудами, фазами и частотами. Таким образом, FFT позволяет нам получить представление о спектральном составе аудиосигнала или любого другого сигнала.
FFT используется во множестве областей, включая аудиообработку, обработку изображений, телекоммуникации и многое другое. С его помощью можно решать такие задачи, как определение частоты звука, удаление шумов из сигнала, анализ спектра сигнала и многое другое.
Быстрое преобразование Фурье является оптимизированной реализацией преобразования Фурье, которая позволяет значительно ускорить процесс вычисления. Оно основано на принципе разделяй и властвуй, разбивая исходную последовательность на две более маленькие последовательности и применяя к ним FFT рекурсивно. Этот процесс повторяется до достижения наименьшей возможной длины последовательности.
Благодаря своей эффективности и мощности, FFT является неотъемлемой частью множества программ и библиотек для аудиообработки и анализа сигналов на языке программирования Python.
Различия между FFT и DFT
Основное различие между FFT и DFT заключается в их алгоритмах обработки данных.
DFT — это преобразование Фурье для дискретных сигналов. Он работает по принципу разбиения сигнала на отдельные временные интервалы и вычисления спектра для каждого из этих интервалов. Основным недостатком DFT является его высокая вычислительная сложность, которая увеличивается пропорционально количеству точек в сигнале.
FFT — это метод для аппроксимации DFT с использованием алгоритма быстрого преобразования Фурье. Он основан на том, что многие вычисления, выполняемые в DFT, могут быть существенно упрощены и сокращены. В результате FFT работает значительно быстрее, чем DFT, особенно при большом количестве точек в сигнале.
FFT широко используется в области обработки аудио и сигналов, так как обеспечивает быструю и эффективную анализ спектра сигналов. Он позволяет определить частоты и амплитуды, присутствующие в сигнале, и использовать эти данные для различных целей, таких как фильтрация шума, сжатие аудиофайлов и многих других.
Таким образом, хотя FFT и DFT оба используются для анализа спектра сигналов, FFT является более эффективным и быстрым методом, который находит свое применение во многих областях, связанных с обработкой сигналов и аудио.
Преобразование временной области в частотную область с помощью FFT
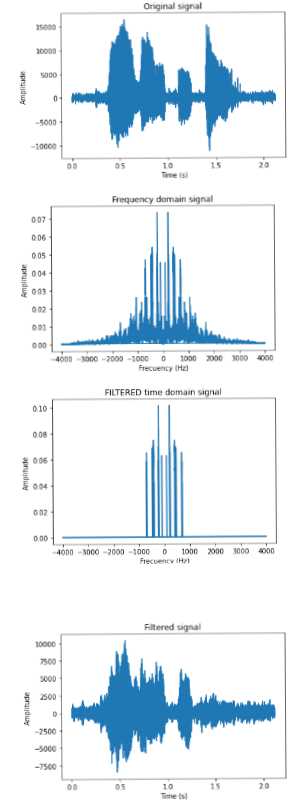
Преобразование временной области в частотную область с помощью FFT позволяет получить график зависимости амплитуды каждой частотной компоненты от ее частоты. Для этого алгоритм разделяет аудиосигнал на небольшие фрагменты временной области, называемые «окнами», и применяет к ним FFT. В результате получается спектрограмма, которая представляет собой двумерную матрицу, где по горизонтальной оси отображается время, а по вертикальной — частота.
Этот метод является очень полезным для анализа и обработки аудиофайлов. Например, с помощью FFT можно определить частоты, на которых присутствуют основные компоненты аудиофайла, такие как голос, музыкальные инструменты и шумы. Также FFT позволяет обнаруживать пики амплитуды на определенных частотах, что может быть полезно при поиске и удалении шумов или помех в аудиозаписи. Кроме того, преобразование временной области в частотную с помощью FFT может быть использовано для создания спектральных анализаторов и эффектов звуковой обработки, таких как эквалайзеры или графические эквалайзеры.
Раздел 2: Основные методы FFT в Python
В Python существует несколько популярных библиотек, которые предоставляют функции для преобразования Фурье (FFT) аудиофайлов. Рассмотрим некоторые из них:
| Библиотека | Описание |
|---|---|
| NumPy | NumPy — это основная библиотека для работы с числовыми данными в Python. Она обладает мощными функциями для выполнения различных математических операций, включая FFT. Основной метод для преобразования Фурье в NumPy — numpy.fft.fft(). |
| SciPy | SciPy — это библиотека, которая расширяет возможности NumPy и предоставляет более специализированные функции для научных вычислений. Она включает в себя модуль scipy.fft, который предоставляет функцию scipy.fft.fft() для выполнения FFT. |
| LibROSA | LibROSA — это библиотека, которая специализируется на анализе аудио и музыки. Она предоставляет удобные функции для работы с аудиофайлами, включая метод librosa.core.stft(), который выполняет кратковременное преобразование Фурье (STFT) и позволяет получить спектрограмму аудио. |
Для выполнения FFT на аудиофайлах с использованием этих библиотек, необходимо предварительно загрузить аудиофайл в формате, поддерживаемом библиотекой (обычно WAV, MP3, OGG и др.), а затем преобразовать аудиофайл в числовой формат, который можно подать на вход функции FFT. После выполнения FFT можно получить спектральные данные, которые могут быть использованы для дальнейшего анализа и обработки аудио.
Библиотеки и модули Python для работы с FFT
Python предлагает различные библиотеки и модули, которые позволяют работать с FFT (быстрым преобразованием Фурье) для анализа аудиофайлов. Ниже представлены некоторые из них:
1. NumPy: Это одна из самых популярных библиотек для работы с научными вычислениями в Python. Включает функцию fft, которая позволяет выполнить FFT над массивом данных. NumPy обладает высокой производительностью и эффективностью обработки больших наборов данных.
2. SciPy: Это библиотека научных и инженерных расчетов, основанная на NumPy. Она содержит различные функции для работы с сигналами, включая функцию fft. SciPy предоставляет более высокоуровневые возможности обработки сигналов, такие как фильтрация и спектральный анализ.
3. matplotlib: Это библиотека графического представления данных, которая также включает функцию для вычисления FFT. Matplotlib позволяет визуализировать спектры частот и анализировать результаты FFT.
4. soundfile: Это модуль Python для чтения и записи аудиофайлов. Он поддерживает различные форматы аудио и предоставляет функции для работы с аудиоданными, включая возможность использования FFT для анализа спектров и преобразования аудиофайлов.
Это лишь некоторые примеры библиотек и модулей Python, которые могут использоваться для работы с FFT. В зависимости от ваших потребностей и задачи, вы можете выбрать наиболее подходящий инструмент для выполнения FFT анализа аудиофайлов в Python.
Примеры кода на Python для реализации FFT
Ниже приведены примеры кода на языке Python, которые позволяют использовать FFT (Быстрое Преобразование Фурье) для анализа аудиофайлов:
- Использование библиотеки NumPy:
- Использование библиотеки SciPy:
- Использование библиотеки librosa:
import numpy as np
# Загрузка аудиофайла
audio_data = np.loadtxt('audio_file.txt')
# Применение FFT
fft_data = np.fft.fft(audio_data)
# Получение амплитудных значений
amplitude = np.abs(fft_data)
# Получение частот
frequency = np.fft.fftfreq(len(amplitude))
print("Амплитуды:", amplitude)
print("Частоты:", frequency)from scipy.fftpack import fft
# Загрузка аудиофайла
audio_data = np.loadtxt('audio_file.txt')
# Применение FFT
fft_data = fft(audio_data)
# Получение амплитудных значений
amplitude = np.abs(fft_data)
# Получение частот
frequency = np.fft.fftfreq(len(amplitude))
print("Амплитуды:", amplitude)
print("Частоты:", frequency)import librosa
# Загрузка аудиофайла
audio_data, sample_rate = librosa.load('audio_file.wav')
# Применение FFT
fft_data = librosa.stft(audio_data)
# Получение амплитудных значений
amplitude = np.abs(fft_data)
# Получение частотных значений
frequency = librosa.fft_frequencies(sr=sample_rate, n_fft=len(amplitude))
print("Амплитуды:", amplitude)
print("Частоты:", frequency)Описанные примеры позволяют загружать аудиофайлы, применять FFT и получать амплитудные и частотные значения. Данные значения могут быть использованы для анализа и визуализации аудио сигналов.
Настройка параметров FFT для оптимального анализа аудиофайлов
Для правильного и эффективного анализа аудиофайлов с использованием FFT (Быстрое преобразование Фурье), необходимо настроить параметры алгоритма в соответствии с требуемыми результатами и характеристиками звука.
Основными параметрами FFT являются:
| Параметр | Описание |
|---|---|
| Размер окна | Определяет размер временного фрагмента аудио, на котором будет проводиться преобразование Фурье. Небольшой размер окна позволяет обнаружить быстро изменяющиеся компоненты звука, но при этом может быть потеряна низкочастотная информация. Большой размер окна обеспечивает более точный анализ низкочастотных компонент, но ухудшает разрешение для высокочастотных компонент. |
| Перекрытие окон | Определяет на сколько процентов окно предыдущего фрагмента перекрывает следующий фрагмент. Перекрытие позволяет сгладить переход между фрагментами и уменьшить артефакты на границах. Оптимальное значение зависит от характеристик аудио и требуемого разрешения. |
| Частотное разрешение | Определяется количеством бинов в спектре после преобразования Фурье. Бин — это отдельная частотная компонента. Частотное разрешение обратно пропорционально размеру окна и определяет насколько маломасштабные изменения в частоте можно обнаружить в аудиофайле. |
| Число битов | Определяет точность значения амплитуды для каждого бина. Чем больше число битов, тем выше точность, но и требуется больше памяти для хранения данных. |
Настраивая данные параметры FFT, можно достичь оптимального сочетания разрешения и точности анализа аудиофайлов. Однако, следует учитывать, что выбор параметров зависит от конкретных требований и особенностей аудио материала, поэтому рекомендуется проводить эксперименты и настраивать параметры в соответствии с конкретной задачей.
Раздел 3: Применение FFT в аудиообработке
Одним из основных применений FFT в аудиообработке является спектральный анализ звуковых сигналов. С помощью FFT можно определить, какие частоты присутствуют в аудиофайле, и как они соотносятся по амплитуде.
FFT также широко используется в задачах обработки и синтеза аудио. Например, с его помощью можно осуществлять фильтрацию звука путем подавления определенных частот или выделения определенных частотных компонент. Также FFT позволяет производить изменение тональности звука и создание эффектов, таких как эхо или реверберация.
Другим интересным применением FFT является распознавание звуковых образов. С помощью анализа спектра звука и его сравнения с предварительно сохраненными образцами можно, например, различать разные голоса или определять музыкальные инструменты.
В области музыки FFT используется для таких задач, как тоновый анализ, настройка инструментов и создание автоматических синтезаторов. С его помощью можно определить оптимальные частоты для настройки струнных или ударных инструментов, а также создать новые звуки путем комбинирования нескольких спектральных компонент.
Современные программы для работы с аудио, такие как аудиоредакторы или программы для создания музыки, обычно предоставляют возможности работы с FFT, что позволяет пользователям осуществлять различные манипуляции с звуком, анализировать и изменять его свойства.
| Применение FFT в аудиообработке: |
|---|
| — Спектральный анализ |
| — Фильтрация звука |
| — Изменение тональности звука |
| — Создание эффектов |
| — Распознавание звуковых образов |
| — Тоновый анализ |
| — Настройка инструментов |
| — Создание новых звуков |




