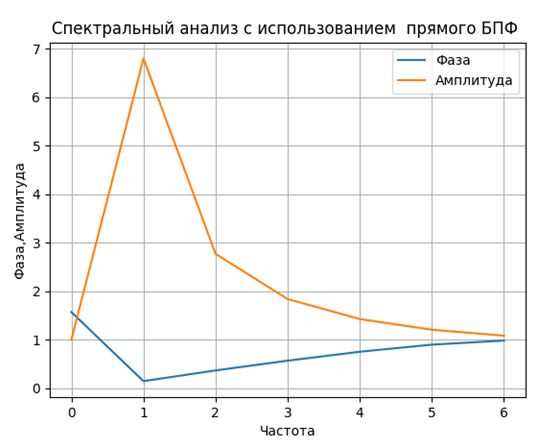
Преобразование Фурье — это незаменимый инструмент в обработке сигналов и анализе данных. В Python есть мощная библиотека NumPy, которая предоставляет широкий функционал для работы с преобразованием Фурье.
Быстрое преобразование Фурье (БПФ) — это эффективный алгоритм для нахождения дискретного преобразования Фурье (ДПФ) последовательности сигналов. Этот алгоритм значительно ускоряет процесс вычисления преобразований Фурье, что делает его особенно полезным в приложениях, требующих высокой скорости и производительности.
В библиотеке NumPy встроена функция fft для выполнения БПФ и функция ifft для выполнения обратного преобразования Фурье (ОПФ). Обе функции предоставляют широкие возможности для работы с преобразованиями Фурье и имеют множество параметров для настройки процесса преобразования.
Python NumPy позволяет легко применять преобразование Фурье к массивам чисел, изображениям и звуковым файлам. Благодаря преобразованию Фурье можно анализировать закономерности данных, выделять частоты сигналов и обрабатывать сигналы в различных областях науки и инженерии. Использование NumPy в Python делает программирование преобразования Фурье более доступным и простым для практического применения и исследований.
Что такое преобразование Фурье?
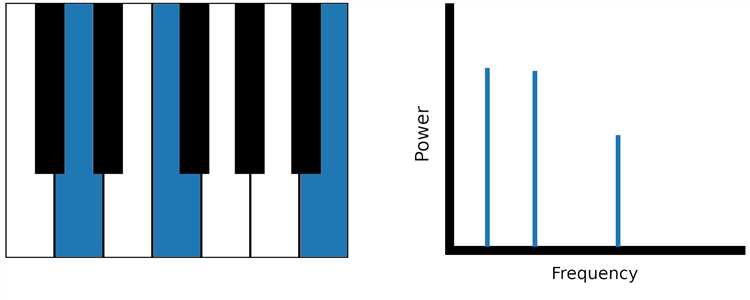
Преобразование Фурье имеет широкое применение в различных областях, включая теорию сигналов и изображений, а также в обработке звука и видео. Оно позволяет анализировать частотные компоненты сигнала и отделять шумы или нежелательные частоты от основного сигнала.
Преобразование Фурье основано на представлении функции в виде интеграла по комплексным экспонентам. Это позволяет представить функцию через ее частотный спектр, который содержит информацию о частотных компонентах и амплитудах каждой из них.
Быстрое преобразование Фурье (Fast Fourier Transform, FFT) – это алгоритм для вычисления преобразования Фурье, который позволяет эффективно обработать большие объемы данных. Он сильно ускоряет вычисления по сравнению с обычным преобразованием Фурье и часто используется в практических приложениях.
Обратное преобразование Фурье (Inverse Fourier Transform) позволяет восстановить исходную функцию из ее частотного представления. Это позволяет преобразовать сигнал обратно из частотной области во временную область.
Использование библиотеки NumPy в языке программирования Python позволяет легко работать с преобразованием Фурье и обратным преобразованием Фурье. Библиотека NumPy предоставляет множество функций для выполнения этих операций и является мощным инструментом для анализа и обработки данных в области сигналов и изображений.
Определение преобразования Фурье
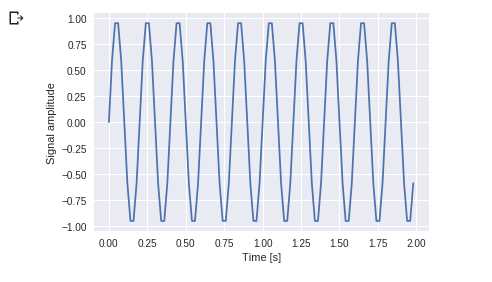
Перед выполнением преобразования Фурье, функция или сигнал описывается как сумма гармонических колебаний различной амплитуды и фазы. Преобразование Фурье позволяет нам перейти от исходных функций или сигналов в пространство частот, где каждая гармоническая составляющая представлена своей амплитудой и фазой.
Преобразование Фурье является базовым инструментом в обработке сигналов и используется во многих областях, включая телекоммуникации, обработку изображений и анализ данных.
Пример использования преобразования Фурье:
Допустим, у нас есть временной ряд данных, представляющий сигнал от источника звука. Используя преобразование Фурье, мы можем разложить этот временной ряд на комплексные компоненты частот, что позволит нам анализировать спектральные характеристики сигнала, такие как основные частоты и амплитуды.
Преобразование Фурье также позволяет нам выполнить обратное преобразование, позволяющее восстановить исходный сигнал из спектральных компонент.
Применение преобразования Фурье в науке и технике
В физике преобразование Фурье используется для анализа электромагнитных волн и спектров атомов, а также для исследования различных физических процессов. Благодаря преобразованию Фурье мы можем описывать и предсказывать поведение сложных систем, таких как квантовые частицы, колебания в механике и электродинамике.
В области обработки сигналов преобразование Фурье находит широкое применение в цифровой обработке звука и изображений. Оно позволяет выделять частотные характеристики сигнала, фильтровать шумы и артефакты, а также улучшать качество звука и изображений. Благодаря преобразованию Фурье мы можем анализировать и модифицировать различные типы сигналов, такие как аудиозаписи, видео и медицинские снимки.
В математике преобразование Фурье играет важную роль в теории дифференциальных уравнений, дискретных системах и обработке данных. Оно позволяет решать сложные задачи связанные с вычислением интегралов, нахождением гармонических компонент и аппроксимацией функций. Благодаря преобразованию Фурье мы можем строить математические модели, описывающие разнообразные явления и процессы.
Преобразование Фурье находит широкое применение также в различных областях техники, таких как телекоммуникации, обработка сигналов, компьютерное зрение и искусственный интеллект. Благодаря преобразованию Фурье мы можем решать задачи связанные с передачей и сжатием данных, распознаванием образов и объектов, а также улучшением качества и эффективности работы различных устройств и систем.
- В физике – анализ электромагнитных волн, спектры атомов и прогнозирование поведения сложных систем.
- В обработке сигналов – цифровая обработка звука и изображений, выделение частотных характеристик, фильтрация шумов.
- В математике – решение уравнений, аппроксимация функций, построение математических моделей.
- В технике – передача и сжатие данных, распознавание образов, улучшение качества и эффективности.
Преобразование Фурье является фундаментальным математическим инструментом, который открывает множество возможностей для анализа и обработки данных в науке и технике. Знание и умение применять преобразование Фурье помогает решать сложные задачи и создавать новые инновационные решения.
Быстрое преобразование Фурье (FFT) в Python NumPy
Функция numpy.fft.fft() может быть использована для выполнения FFT на одномерном массиве или последовательности чисел. Она принимает один обязательный аргумент — входные данные, и возвращает массив комплексных чисел с преобразованными значениями.
Пример использования функции numpy.fft.fft():
«`python
import numpy as np
# Входной сигнал
x = np.array([1, 2, 3, 4])
# Выполнение FFT
y = np.fft.fft(x)
print(y)
Результат:
[10.+0.j -2.+2.j -2.+0.j -2.-2.j]
Функция numpy.fft.ifft() используется для выполнения обратного преобразования Фурье. Она принимает массив комплексных чисел и возвращает восстановленные значения сигнала.
Пример использования функции numpy.fft.ifft():
«`python
import numpy as np
# Входной спектр
y = np.array([10.+0.j, -2.+2.j, -2.+0.j, -2.-2.j])
# Выполнение обратного преобразования Фурье
x = np.fft.ifft(y)
print(x)
Результат:
[1.-2.55269432e-17j 2.-2.55269432e-17j 3.-2.55269432e-17j 4.-2.55269432e-17j]
Библиотека NumPy также предлагает возможность применения быстрого преобразования Фурье в двумерном пространстве с помощью функции numpy.fft.fftn(), и обратного преобразования Фурье с помощью функции numpy.fft.ifftn(). Эти функции работают с многомерными массивами и предоставляют возможности анализа и обработки изображений, аудио и других типов данных.
Пример использования numpy.fft.fftn():
«`python
import numpy as np
# Входная матрица
x = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Выполнение FFT на двумерном пространстве
y = np.fft.fftn(x)
print(y)
Результат:
[[45.+0.j -4.+2.59807621j -4.-2.59807621j]
[-9.+9.12716475j 0.+0.j -1.+1.73205081j]
[-9.-9.12716475j -1.-1.73205081j 0.+0.j ]]
Как видно из примеров, использование функций быстрого преобразования Фурье (FFT) в NumPy позволяет легко выполнять преобразование сигналов, анализировать и обрабатывать данные с использованием пространства частот и обратно.
Обзор библиотеки NumPy
Основным объектом NumPy является массив (ndarray), который представляет собой многомерный контейнер для элементов одного типа данных. Массивы NumPy более эффективны по сравнению с обычными списками Python благодаря своей оптимизированной реализации на языке C и использованию векторизованных операций.
Библиотека NumPy предоставляет множество функций для работы с массивами, включая:
| Функция | Описание |
|---|---|
| numpy.array() | Создание массива |
| numpy.zeros() | Создание массива нулей |
| numpy.ones() | Создание массива единиц |
| numpy.arange() | Создание последовательности чисел |
| numpy.linspace() | Создание равномерно распределенной последовательности чисел |
Кроме того, NumPy предоставляет функции для выполнения математических операций над массивами, таких как сложение, вычитание, умножение, деление и другие. Библиотека также поддерживает работу с многомерными массивами и предоставляет удобные инструменты для их манипуляции, включая изменение формы, изменение размерности, транспонирование и другие.
NumPy имеет широкий спектр применений, включая научные исследования, статистику, машинное обучение, обработку изображений, обработку сигналов и другие области. Благодаря своей эффективности и богатым возможностям, она является одной из самых популярных библиотек для работы с массивами и математическими вычислениями в Python.
Алгоритм быстрого преобразования Фурье (FFT) в NumPy
NumPy предоставляет функцию numpy.fft.fft(), которая реализует алгоритм FFT. Данная функция принимает одномерный или двумерный массив в качестве входных данных и возвращает преобразованный массив в соответствии с положительными и отрицательными частотами.
Алгоритм FFT является эффективным способом вычисления преобразования Фурье, поскольку его сложность составляет O(N log N), где N — количество элементов преобразуемого массива. Таким образом, FFT позволяет эффективно обрабатывать массивы большого размера за разумное время. Это делает его особенно полезным при работе с большими объемами данных.
Для использования функции numpy.fft.fft() необходимо импортировать модуль numpy.fft. Затем можно вызывать функцию, указывая входной массив в качестве аргумента:
import numpy as np
from numpy.fft import fft
data = np.array([1, 2, 3, 4])
transformed_data = fft(data)
print(transformed_data)
В результате выполнения кода будет выведен преобразованный массив, содержащий значения комплексных чисел, представляющих положительные и отрицательные частоты. Если необходимо получить только положительные частоты, можно использовать функцию numpy.fft.fftshift().
Алгоритм быстрого преобразования Фурье в NumPy является мощным инструментом для обработки и анализа данных. Благодаря его эффективности и простоте использования он позволяет решать сложные задачи связанные с преобразованием Фурье в удобной и эффективной форме.
Пример использования FFT в Python NumPy
Библиотека NumPy в Python предоставляет удобный инструментарий для работы с преобразованием Фурье. Преобразование Фурье позволяет анализировать частотный состав сигнала и применяется в различных областях, таких как цифровая обработка сигналов, изображений, аудио, телекоммуникации и других.
Примером использования FFT (быстрое преобразование Фурье) в NumPy может быть анализ временного ряда данных. Предположим, у нас есть временной ряд, представленный в виде массива значений. Мы хотим узнать, какие частоты присутствуют в этом временном ряде.
Для начала, импортируем библиотеки NumPy и Matplotlib:
import numpy as np
import matplotlib.pyplot as plt
Затем создадим массив значений временного ряда. В данном примере, для удобства, будем использовать значения синусоиды с частотой 1 Гц:
time = np.linspace(0, 1, 1000) # временная ось от 0 до 1 секунды
frequency = 1 # частота сигнала 1 Гц
signal = np.sin(2 * np.pi * frequency * time) # сигнал с частотой 1 Гц
Полученный сигнал, представленный в виде массива значений, можно визуализировать с помощью библиотеки Matplotlib:
plt.plot(time, signal)
plt.xlabel('Время, сек')
plt.ylabel('Амплитуда')
plt.show()
Теперь мы можем применить FFT к нашему сигналу с помощью функции np.fft.fft(). Эта функция возвращает амплитудный спектр сигнала:
amplitude_spectrum = np.fft.fft(signal)
Чтобы получить информацию о частотах, связанных с каждым элементом спектра, можно использовать функцию np.fft.fftfreq():
frequency_spectrum = np.fft.fftfreq(len(signal), d = time[1] - time[0])
Наконец, можно визуализировать амплитудный спектр:
plt.plot(frequency_spectrum, np.abs(amplitude_spectrum))
plt.xlabel('Частота, Гц')
plt.ylabel('Амплитуда')
plt.show()
Таким образом, мы получаем график амплитудного спектра нашего сигнала, который позволяет нам увидеть, какие частоты присутствуют в нем. Этот пример демонстрирует базовый подход к использованию FFT в Python NumPy для анализа временных рядов.



